- Update 21.04.2020: The code still works, but only if you set the account language to English.
- Update 23.11.2019: There are reports that Twitter started to prevent the automated unblocking of accounts. After some 50 to 100 unblocks, the page with blocked accounts get blocked. As a result the script may currently not work.
- Update 17.11.2019: The old code only worked in Firefox. I updated it to work in Chrome as well.
- Update 12.07.2019: NewTwitter also known as Twitter Web has a completely new interface. I updated the code accordingly.
If you have blocked hundreds of accounts, unblocking them one by one takes a lot of time. But there is a quick and easy way to unblock them all at once. You don’t need to give any app write permissions to your account for it to work.
Short version
Got to the blocked accounts setting page and enter the following code. It will unblock all visible accounts.
document.querySelectorAll('[aria-label="Blocked"]').forEach(function(account) {
account.click()
});Long version
1. Go to the settings
On this page you see all accounts your are blocking at the moment:
https://twitter.com/settings/blocked

2. Open the Developer Tools
Quickest way: Press F12 on Windows/Linux or Command+Option+I on MacOS. Tested on Chrome and Firefox.
You can go through the menu as well. Firefox: Extras -> Web Developers. Chrome: Other Tools -> Developer Tools.
You should now see a new area in your browser. Either on the right side or on the bottom of the window.
3. Open the Browser Console
Either by pressing “Esc” or selecting it in the top menu of the developer tools. With the console you can execute any JavaScript commands.
4. Execute autoUnblock-snippet in the browser console
The Twitter web interface got a new design. NewTwitter (also known as Twitter Web App) is written in React and it unloads elements while scrolling. Because of that we need to scroll just a bit, unblock all visible accounts, scroll again, unblock some more and so on.
The following code sets up an interval which fires every second (1000 milliseconds). After each second it scrolls down one page, selects all unblockable accounts and clicks the unblock button.
let autoUnblock = setInterval(function() {
window.scrollBy(0, window.innerHeight);
document.querySelectorAll('[aria-label="Blocked"]').forEach(function(account) {
account.click()
});
}, 1000);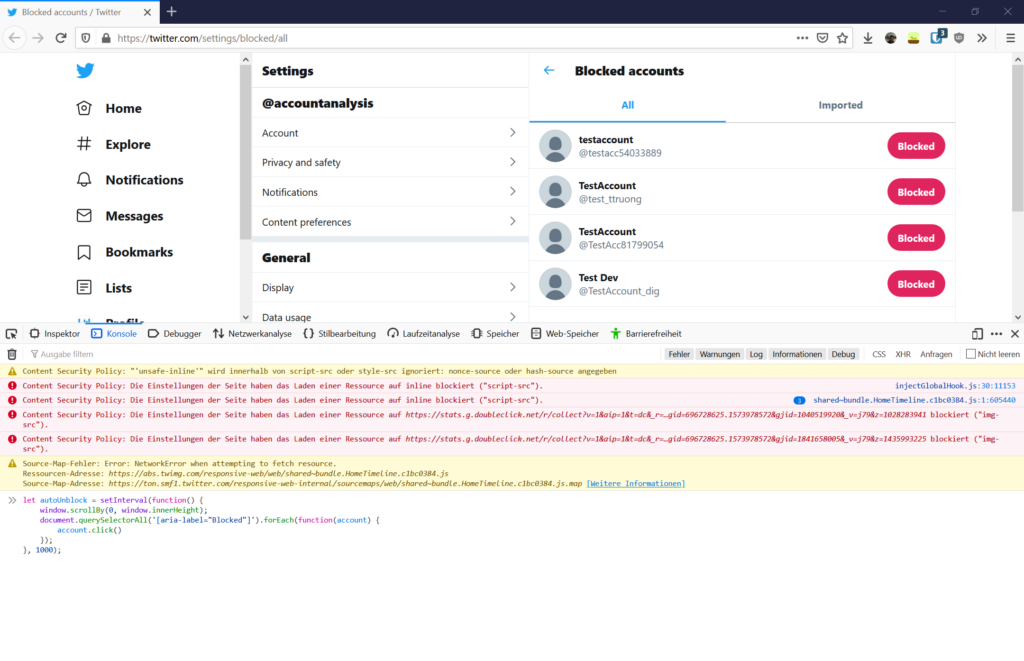
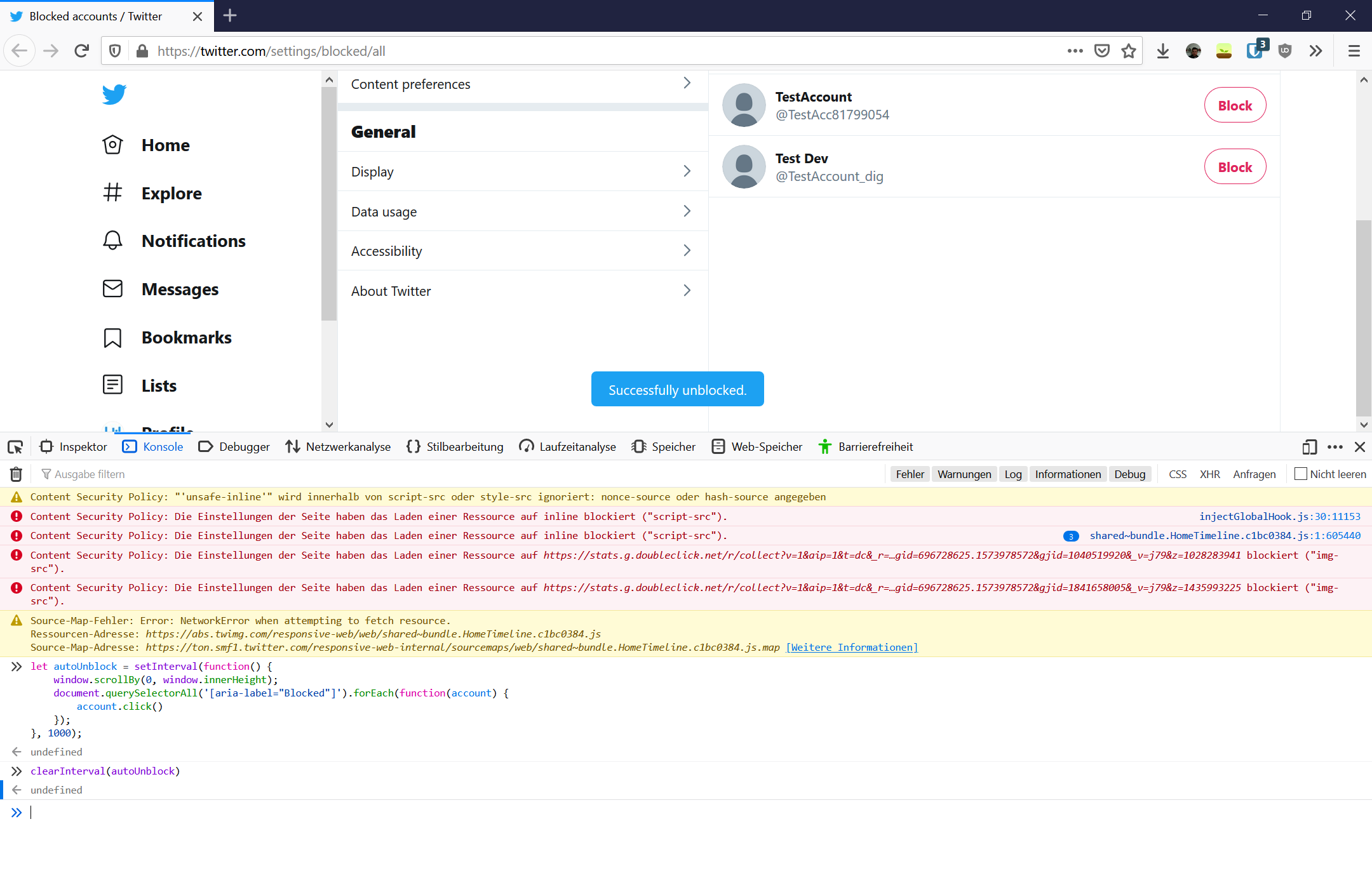
5. Stop the autoUnblocker once it’s done
Once all accounts are unblocked, you can stop it by executing the following code in the browser console. Alternatively, just close the browser tab.
clearInterval(autoUnblock)
Done
All accounts should now be unblocked. If you have any questions, let me know on Twitter.
Optional one-time reversal of the process
With the new code you can’t accidentally follow the once blocked accounts anymore. That’s great. Additionally it is possible to block them again. But only while the browser tab is open. Once the tab is closed, the list of accounts is gone.
Execute the following snippet to block all the accounts you just unblocked. The only change is from ‘Blocked’ to ‘Block’ in the aria-label.
let autoBlock = setInterval(function() {
window.scrollBy(0, window.innerHeight);
document.querySelectorAll('[aria-label="Block"]').forEach(function(account) {
account.click()
});
}, 1000);This code needs to be stopped as well.
clearInterval(autoBlock)Bonus: Unmute all muted accounts
Some people asked me how to umute all accounts they ever muted. With the new code snippet that’s easy as well.
Go to the settings page with the muted accounts: https://mobile.twitter.com/settings/muted/all
let autoUnmute = setInterval(function() {
window.scrollBy(0, window.innerHeight);
document.querySelectorAll('[aria-label^="Unmute"]').forEach(function(account) {
account.click()
});
}, 1000);Once all accounts are unmuted, stop it:
clearInterval(autoUnmute)To reverse it (only while possible while you haven’t left the page), change the name from ‘autoUnmute’ to ‘autoMute’ (or anything else) and replace ‘[aria-label^=”Unmute”] with ‘[aria-label^=”Mute”]’.
Technical explanation: The ‘ ^ ‘ is necessary because the aria-labels for Muting/Unmuting contain the account name. ‘ ^ ‘ says, that the aria-label starts with the phrase, but it can contain other stuff. For the blocked accounts that isn’t necessary because they all have the same aria-label.
Leave a Reply